Таково полезное использование простой, казалось бы, игрушки.

Многие удивительные фокусы разнообразной программы жонглеров основаны тоже на свойстве вращающихся тел сохранять направление оси вращения. Позволю себе привести выдержку из увлекательной книги английского физика проф. Джона Перри «Вращающийся волчок».

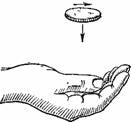
Рисунок 28. Как летит монета, подброшенная с вращением.

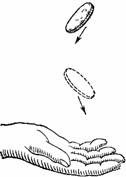
Рисунок 29. Монета, подброшенная без вращения, падает в случайном положении.

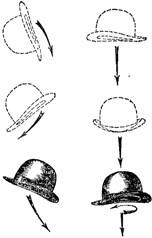
Рисунок 30. Подброшенную шляпу легче поймать, если ей было сообщено вращение около оси.

«Однажды я показывал некоторые из моих опытов перед публикой, пившей кофе и курившей табак в великолепном помещении концертного зала „Виктория“ в Лондоне. Я старался заинтересовать моих слушателей, насколько мог, и рассказывал о том, что плоскому кольцу надо сообщить вращение, если его желают бросить так, чтобы можно было наперед указать, куда оно упадет; точно так же поступают, если хотят кому-нибудь бросить шляпу так, чтобы он мог поймать этот предмет палкой. Всегда можно полагаться на сопротивление, которое оказывает вращающееся тело, когда изменяют направление его оси. Далее я объяснял моим слушателям, что, отполировав гладко дуло пушки, никогда нельзя рассчитывать на точность прицела; вследствие этого теперь делают нарезные дула, т. е. вырезают на внутренней стороне дула пушек спиралеобразные желоба, в которые приходятся выступы ядра или снаряда, так что последний должен получить вращательное движение, когда сила взрыва пороха заставляет его двигаться по каналу пушки. Благодаря этому снаряд покидает пушку с точно определенным вращательным движением.

Это было все, что я мог сделать во время этой лекции, так как я не обладаю ловкостью в метании шляп или дисков. Но после того, как я закончил свою лекцию, на подмостки выступили два жонглера, — и я не мог пожелать лучшей иллюстрации упомянутых выше законов, нежели та, которую давал каждый отдельный фокус, показанный этими двумя артистами. Они бросали друг другу вращающиеся шляпы, обручи, тарелки, зонтики… Один из жонглеров бросал в воздух целый ряд ножей, ловил их опять и снова подбрасывал с большой точностью вверх; моя аудитория, только что прослушав объяснение этих явлений, ликовала от удовольствия; она замечала вращение, которое жонглер сообщал каждому ножу, выпуская его из рук так, что мог наверное знать, в каком положении нож снова вернется к нему. Я был тогда поражен, что почти все без исключения жонглерские фокусы, показанные в тот вечер, представляли иллюстрацию изложенного выше принципа».

Свою знаменитую задачу о том, как поставить яйцо, Колумб решил чересчур просто: надломил его скорлупу [12] . Такое решение, в сущности, неверно: надломив скорлупу яйца, Колумб изменил его форму и, значит, поставил не яйцо, а другое тело; ведь вся суть задачи в форме яйца: изменяя форму, мы заменяем яйцо другим телом. Колумб дал решение не для того тела, для которого оно искалось.

Рисунок 31. Решение колумбовой задачи: яйцо вращается, стоя на конце.

А между тем можно решить задачу великого мореплавателя, нисколько не изменяя формы яйца, если воспользоваться свойством волчка; для этого достаточно только привести яйцо во вращательное движение вокруг его длинной оси, — и оно будет, не опрокидываясь, стоять некоторое время на тупом или даже на остром конце. Как это сделать — показывает Рисунок : яйцу придают вращательное движение пальцами. Отняв руки, вы увидите, что яйцо продолжает еще некоторое время вращаться стоймя: задача решена.

Для опыта необходимо брать непременно вареные яйца. Это ограничение не противоречит условию колумбовой задачи: предложив ее, Колумб взял яйцо тут же со стола, а к столу, надо полагать, поданы были не сырые яйца. Вам едва ли удастся заставить стоймя вращаться яйцо сырое, потому что внутренняя жидкая масса является в данном случае тормозом. В этом, между прочим, состоит простой способ отличать сырые яйца от сваренных вкрутую — прием, известный многим хозяйкам.

«Вода не выливается из сосуда, который вращается, — не выливается даже тогда, когда сосуд перевернут дном вверх, ибо этому мешает вращение», — писал две тысячи лет назад Аристотель. На рис. 32 изображен этот эффектный опыт, который, без сомнения, многим знаком: вращая достаточно быстро ведерко с водой, как показано на рисунке, вы достигаете того, что вода не выливается даже в той части пути, где ведерко опрокинуто вверх дном.

В обиходе принято объяснять это явление «центробежной силой», понимая под нею ту воображаемую силу, которая будто бы приложена к телу и обусловливает стремление его удалиться от центра вращения. Этой силы не существует: указанное стремление есть не что иное, как проявление инерции, а всякое движение по инерции осуществляется без участия силы. В физике под центробежной силой разумеют нечто иное, а именно — ту реальную силу, с какой вращающееся тело натягивает удерживающую его нить или давит на свой криволинейный путь. Сила эта приложена не к движущемуся телу, а к препятствию, мешающему ему двигаться прямолинейно: к нити, к рельсам на кривом участке пути и т. п.

Обращаясь к вращению ведерка, попытаемся разобраться в причине этого явления, не прибегая вовсе к двусмысленному понятию «центробежной силы». Зададим себе вопрос: куда направится струя воды, если в стенке ведерка сделать отверстие? Не будь силы тяжести, водяная струя по инерции направилась бы по касательной АК к окружности АВ (рис. 32). Тяжесть же заставляет струю снижаться и описывать кривую (параболу АР). Если окружная скорость достаточно велика, эта кривая расположится вне окружности АВ. Струя обнаруживает перед нами тот путь, по которому при вращении ведерка двигалась бы вода, если бы не препятствовало надавливающее на нее ведерко. Теперь понятно, что вода вовсе не стремится двигаться отвесно вниз, а потому и но выливается из ведерка. Она могла бы вылиться из него лишь в том случае, если бы ведерко было обращено отверстием в направлении его вращения.

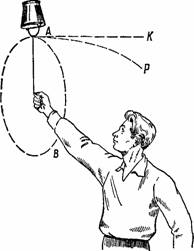
Рисунок 32. Почему не выливается вода из вращаемого ведерка?

Вычислите теперь, с какой скоростью надо в этом опыте вращать ведерко, чтобы вода из него не выливалась вниз. Скорость эта должна быть такова, чтобы центростремительное ускорение вращающегося ведерка было не меньше ускорения силы тяжести: тогда путь, по которому стремится двигаться вода, будет лежать вне окружности, описываемой ведерком, и вода нигде от ведерка не отстанет. Формула для вычисления центростремительного ускорения W такова;

W=v2/R,

где v — окружная скорость, R — радиус кругового пути. Так как ускорение тяжести на земной поверхности g = 9,8 м/сек2, то имеем неравенство v2/R»= 9,8. Если положить R равным 70 см, то

и v»= 2,6 м/сек.

Легко рассчитать, что для получения такой окружной скорости надо делать рукой около полутора оборотов в секунду. Подобная быстрота вращения вполне достижима, и опыт удается без труда.

Способностью жидкости прижиматься к стенкам сосуда, в котором она вращается вокруг горизонтальной оси, пользуются в технике для так называемого центробежного литья. При этом имеет существенное значение то, что неоднородная жидкость расслаивается по удельному весу: более тяжелые составные части располагаются дальше от оси вращения, легкие занимают место ближе к оси. Вследствие этого все газы, содержащиеся в расплавленном металле и образующие так называемые «раковины» в литье, выделяются из металла во внутреннюю, полую часть отливки. Изделия, изготовленные таким способом, получаются плотные и свободные от раковин. Центробежное литье дешевле обычного литья под давлением и не требует сложного оборудования.